A lire sur: http://www.futura-sciences.com/magazines/espace/infos/actu/d/univers-modele-testable-energie-noire-12-piste-kaluza-klein-46851/#xtor=EPR-17-[QUOTIDIENNE]-20130704-[ACTU-Modele-testable-d-energie-noire--1/2--:-la-piste-de-Kaluza-Klein]
 Albert Einstein a fini par considérer que
l'introduction de sa constante cosmologique dans le premier modèle
d'univers relativiste était la plus grande erreur de sa vie.
Aujourd'hui, avec la découverte de l'énergie noire, c'est un témoignage
de plus de son génie. © Yousuf Karsh
Albert Einstein a fini par considérer que
l'introduction de sa constante cosmologique dans le premier modèle
d'univers relativiste était la plus grande erreur de sa vie.
Aujourd'hui, avec la découverte de l'énergie noire, c'est un témoignage
de plus de son génie. © Yousuf Karsh

Le grand physicien et cosmologiste biélorusse Yakov Zel'dovich avait pris très au sérieux la constante cosmologique d'Einstein. Pour lui, elle devait être une manifestation de l'énergie du vide quantique. © www.astronet.ru

Theodor Kaluza (à gauche) et Oscar Klein. Kaluza a proposé sa théorie en 1919. Elle n'unifiait que les forces connues de l'époque, à savoir la gravitation et l'électromagnétisme. Klein est allé plus loin dans les années 1930 en complétant les idées de Kaluza et en utilisant les lois de la mécanique quantique. © Stanley Deser, Université de Göttingen



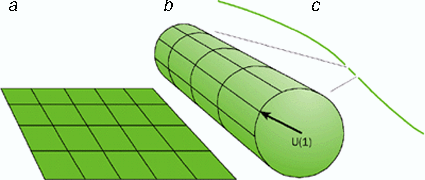
Une surface enroulée et compactifiée sous forme d'un cylindre ressemble de loin à un objet à une dimension, une ligne. Le groupe de rotation déplaçant un point d'un cercle en un autre est le groupe de Lie U(1). © physicsweb
La nature de
l'énergie noire accélérant l'expansion de l'univers observable est l'une
des plus grandes énigmes de la physique. Des chercheurs français, Alain
Blanchard (Irap), Arnaud Dupays (Irap) et Brahim Lamine (LKB) viennent
de proposer un nouveau modèle à son sujet. Pour reproduire la valeur de
la constante cosmologique observée, ils introduisent une dimension
spatiale supplémentaire, comme Kaluza et Klein avant eux, ainsi qu'une
variante de l'effet Casimir. Futura-Sciences y reviendra bientôt avec
Alain Blanchard.
Le 03/07/2013 à 09:33
- Par
 Albert Einstein a fini par considérer que
l'introduction de sa constante cosmologique dans le premier modèle
d'univers relativiste était la plus grande erreur de sa vie.
Aujourd'hui, avec la découverte de l'énergie noire, c'est un témoignage
de plus de son génie. © Yousuf Karsh
Albert Einstein a fini par considérer que
l'introduction de sa constante cosmologique dans le premier modèle
d'univers relativiste était la plus grande erreur de sa vie.
Aujourd'hui, avec la découverte de l'énergie noire, c'est un témoignage
de plus de son génie. © Yousuf Karsh
La découverte de l’expansion accélérée de l’univers a été une surprise. Elle implique qu’il faut réintroduire dans les équations de la relativité générale la fameuse constante dont Einstein
s’était servi en 1917 pour construire son modèle cosmologique. À
l’époque, Einstein cherchait surtout à résoudre divers problèmes liés au
principe de Mach et
à la détermination des solutions de ses équations. L’objectif n’était
pas tellement, comme on le dit trop souvent, d’obtenir un modèle
décrivant un univers statique, fini et éternel (bien que ces aspects de
son modèle cosmologique n’étaient pas pour lui déplaire).
À la fin des années 1960, Yakov Zel’dovich
interpréta la constante cosmologique d’Einstein comme un effet de
l’énergie du vide quantique, c'est-à-dire l’état d’énergie minimale des
champs quantiques avec leurs fluctuations incessantes causées par les
inégalités d’Heisenberg. Malheureusement, comme l’avait déjà très bien
compris Pauli avant lui, la valeur de l’énergie du vide devait être si
fantastiquement élevée que l’univers aurait dû se recourber sur lui-même
et avoir une taille bien inférieure à celle du Système solaire. C’est
ce que l’on appelle la pire prédiction de la physique théorique.
La mystérieuse nature de la constante cosmologique
Toutefois, on pouvait arriver à annuler la valeur de
l’énergie du vide en faisant des contorsions théoriques. Mais lorsque
Saul Perlmutter et ses collègues se sont rendu compte que la valeur de
la constante cosmologique d’Einstein n’était pas nulle, bien que très
faible, les calculs menés pour expliquer cette faible valeur sont
devenus encore plus problématiques.

Le grand physicien et cosmologiste biélorusse Yakov Zel'dovich avait pris très au sérieux la constante cosmologique d'Einstein. Pour lui, elle devait être une manifestation de l'énergie du vide quantique. © www.astronet.ru
Bien des théories sont apparues pour tenter
d’expliquer la nature de l’énergie noire accélérant l’expansion de
l’univers via la constante d’Einstein. On en est même venu à penser que
cette énergie pouvait varier dans le temps et l’espace, ce qu’en fait
Einstein et Schrödinger savaient déjà. Pour tenter d’y voir plus clair, le prix Nobel de physique Martin Perl a proposé de tester certains de ces modèles d’énergie noire en laboratoire. Comme l’avait expliqué Saul Perlmutter, il y a aussi des projets comme le Large Synoptic Survey Telescope (LSST) et le satellite de l’Esa, Euclid, qui se proposent de faire la lumière sur la nature de l’énergie noire.
Énergie du vide et contraintes cosmologiques
Récemment, un groupe de chercheurs français composé
d’Alain Blanchard (IRAP), Arnaud Dupays (IRAP) et Brahim Lamine a
proposé un intéressant modèle de l’énergie noire basé sur une nouvelle
façon d’aborder le calcul de la valeur de l’énergie du vide quantique en
tenant compte des contraintes de la cosmologie. Ce modèle repose aussi
sur l’existence d’une dimension spatiale supplémentaire, du type de
celle déjà introduite dans les fameuses théories de Kaluza-Klein,
lourdement utilisées par la théorie des supercordes.
Ce modèle fait des prédictions précises, notamment
que l’énergie noire doit se comporter comme une vraie constante
cosmologique, comme le pense, par exemple, Jean-Pierre Luminet.
Une autre de ces prédictions devrait bientôt pouvoir être testée en
laboratoire. Celle qui est la plus facilement vérifiable est tout
simplement le fait que les trois physiciens arrivent à retrouver la
valeur de la constante cosmologique observée.
Équations de Kaluza-Klein et effet Casimir
Futura-Sciences a demandé à Alain Blanchard de nous en dire plus sur ce modèle d’énergie du vide quantique, qui fait de plus un lien avec l’effet Casimir.
Mais avant de lui laisser la parole, un petit détour par les théories
de Kaluza-Klein s’impose, pour mieux comprendre ce qu’elles sont.
Comprendre ce qu’Alain Blanchard, Arnaud Dupays et
Brahim Lamine ont fait n'est pas aussi difficile qu'on pourrait le
croire, même si cela nécessite un peu de travail. Cet article se propose
donc de mener le lecteur à travers une petite « excursion en
montagne ». Il y aura quelques équations, mais que personne ne
s'effraie, il n'y aura pas besoin de maîtriser la physique ou les
mathématiques qui tournent autour pour les comprendre, de même qu'il n'y
a pas besoin de savoir peindre comme Michel-Ange pour analyser et
comprendre une de ses peintures. Elles ne seront là que pour faire
passer des idées et donner un aperçu de l'univers des physiciens
théoriciens.
On ne dissimulera pas quand même le fait que la consultation des dossiers de Futura-Sciences sur la relativité générale et la théorie des trous de ver pourrait
bien être nécessaire pour certains. En outre, ces dossiers possèdent
des liens permettant d'approfondir bien des points sur la relativité
générale.
Une théorie purement géométrique des forces de la nature
Pour bien comprendre les problèmes auxquels les physiciens ont été confrontés, il faut remonter aux premières tentatives de théorie unitaire,
celles d'Einstein et Kaluza-Klein. Dans le cadre de la théorie de
Kaluza-Klein, en étendant le nombre de dimensions spatiales de l'espace,
on arrive à donner une interprétation géométrique de toutes les forces,
et pas seulement de la gravitation, à partir de la géométrie-topologie de l'espace-temps.

Theodor Kaluza (à gauche) et Oscar Klein. Kaluza a proposé sa théorie en 1919. Elle n'unifiait que les forces connues de l'époque, à savoir la gravitation et l'électromagnétisme. Klein est allé plus loin dans les années 1930 en complétant les idées de Kaluza et en utilisant les lois de la mécanique quantique. © Stanley Deser, Université de Göttingen
Si l'on considère les équations d'Einstein reliant
la courbure de l'espace-temps à une distribution d'énergie et
d'impulsion, elles s'écriront, dans le cas où la source du champ de
gravitation est un champ électromagnétique, sous la forme suivante :
Le membre de gauche fait intervenir la géométrie de
l'espace-temps. Il est construit à partir des dérivées spatiales et
temporelles de la métrique de cet espace-temps.
Le membre de droite, lui, fait intervenir ce qu'on appelle le tenseur
impulsion-énergie des sources du champ de gravitation. Ici, il s'agit
d'un champ électromagnétique (em) pur. Dans le vide, les équations
précédentes se réduiraient à l'équation donnée par l'annulation du
tenseur de courbure contracté, dit tenseur de Ricci :
La magie de la théorie de Kaluza-Klein est qu'en
écrivant cette dernière équation pour un espace-temps à cinq dimensions
avec une dimension d'espace supplémentaire compactifiée sous forme de
cercle, on retombe sur les équations du champ de gravitation en quatre
dimensions couplées à un champ électromagnétique gouverné par les
équations de Maxwell ! On a donc les équations ci-dessous :
Le processus peut être généralisé, en ajoutant à notre espace-temps macroscopique à quatre dimensions des espaces géométriques microscopiques « internes » à n
dimensions pour chaque point de cet espace. Ces dimensions
supplémentaires doivent être compactifiées et de très petites tailles
pour être compatibles avec le fait qu'on ne détecte pas ordinairement
des dimensions spatiales de plus dans lesquelles les atomes pourraient se déplacer.
Une clé pour l'unification : les symétries géométriques
Les symétries géométriques des dimensions
supplémentaires donnent alors les types de groupes de jauge associés aux
forces et aux particules. Ce sont des groupes de Lie, dont l'importance
en physique et en mathématiques ne saurait être sous-estimée. On voit là une nouvelle illustration de l'importance des symétries et de la théorie des groupes en physique.
Ainsi, selon une dimension supplémentaire donnant un
cercle, la conservation de l'impulsion d'une particule le long de cette
dimension compacte découle de l'invariance par rotation des équations
selon ce cercle. Il se trouve que cette loi de conservation en cinq
dimensions se traduit par la loi de conservation de la charge électrique
en quatre dimensions associée au groupe de Lie U(1) des équations de Maxwell.

Une surface enroulée et compactifiée sous forme d'un cylindre ressemble de loin à un objet à une dimension, une ligne. Le groupe de rotation déplaçant un point d'un cercle en un autre est le groupe de Lie U(1). © physicsweb
Si on avait une n-sphère, on en sortirait SU(2), SU(3) etc. Et donc, à chaque fois, la conservation des charges de QED, QCD,
et autres correspond juste à la conservation de l'impulsion en
dimensions supplémentaires. Ces charges donnent aussi la valeur de la
constante de couplage de ces interactions en liaison avec la géométrie
et la taille des dimensions supplémentaires. Après ces prolégomènes,
nous nous tournerons vers les explications d'Alain Blanchard dans
l'interview qui suivra cet article.